MATEMATICAS GRADO DECIMO
APUNTES PARA TRIGONOMETRIA: Recordando el Álgebra
Por Helena hernández Millán
POLINOMIOS:
TERMINOS SEMEJANTES: Expresiones algebraicas con la misma parte literal afectada por los mismos exponentes. Para reducirlas se suman algebraicamente sus coeficientes y su parte literal se conserva igual.
Ejemplo: -5X4 + 8X4= 3X4
PRODUCTO DE EXPRESIONES ALGEBRAICAS: se multiplican los coeficientes (teniendo en cuenta sus signos) y los exponentes de la parte literal se suman.
EJEMPLO: (-6X3Y7)(9X5Y-3)= -54X8Y4
(3X5-4X)(-2X3)= -6X8 + 8X4
PRODUCTOS NOTABLES:
Binomio al cuadrado: (a ± b)2 = a2 ± 2ab + b2 Ej: (X – 3)2 = X2 – 6X + 9
Binomio al Cubo: (a ± b)3 = a3 ± 3a2b + 3ab2 ± b3 Ej: (X – 2)3= X3 – 3(X2)(2) + 3X(22) – 23 = X3-6X2+12X -8
Suma por Diferencia: (a + b)(a – b) = a2- b2 Ej: (4X3 + 3X) (4X3 - 3X)= 16X6 – 9X2
COCIENTES NOTABLES:
FACTORIZACIÓN: Factorizar significa expresar un polinomio como un producto de dos o más expresiones
Factor Común: Cuando todos los términos del polinomio tienen un factor común, es decir un divisor que aparece en todos los términos. En el coeficiente corresponde al máximo común divisor y en la parte literal común, a la de menor exponente.
Ejemplo: Factorizar 8X3Y3Z – 24X6Y4 + 12X2Y7Z2 = 4X2Y3(2XZ – 6X4Y + 3Y4Z2)
Diferencia de Cuadrados: Ocurre cuando aparece una diferencia (resta) de dos expresiones que sean cuadrados perfectos. Se factoriza como la suma por la diferencia de las raíces de las dos expresiones.
Ejemplo: X2 – Y2 = (X + Y)(X – Y) 16a2 – 25b6 = (4a + 5b3)(4a – 5b3)
Trinomio Cuadrado perfecto: Ocurre cuando el polinomio corresponde al desarrollo de un binomio al cuadrado. Para comprobar que estamos en este caso se extrae la raíz cuadrada del primer y tercer términos (que siempre deben ser positivos) y se duplica el producto de estas dos raíces. Si este resultado coincide con el segundo término del trinomio entonces si es cuadrado perfecto. Se factoriza como un binomio con las dos raíces y signo del segundo término elevado al cuadrado.
Trinomio de la forma X2+BX + C: Se factorizan buscando dos números que multiplicados den el término independiente y sumados (teniendo en cuenta el signo) den el coeficiente del segundo término. En cada paréntesis se inicia con la raíz del primer término del trinomio, luego signo del segundo para el primer factor y, producto de segundo y tercer términos, y a continuación los dos números encontrados.
X2 – 9X + 20 = (X – 5)(X – 4)
Trinomio de la forma AX2+BX + C: Se diferencian de los trinomios del caso anterior porque el primer término tiene un coeficiente distinto de 1. Para factorizarlo se multiplica todo el trinomio por el coeficiente del primer término, cuidando de dejar indicado el producto en el segundo término, y se debe dividir por este mismo número. De esta manera se reduce a un trinomio de la forma X2 +BX + C, ya que el primer término aparece como un cuadrado perfecto.
Ej: factorizar 2X2 + 11X + 5
Multiplicamos por 2 el trinomio, dejando indicado en el segundo (la expresión del paréntesis corresponde a la raíz del primer término, así: 4X2 + 11(2X) + 10.
Luego se buscan dos números que multiplicados sean 10 y sumados 11. Se factoriza dejando en cada factor la raíz cuadrada del primer término de este nuevo trinomio. No olvidar dividir por el número que se multiplicó:
Diferencia de Cubos: a3 – b3 = (a – b)(a2 + ab + b2)
Suma de Cubos: a3 + b3 = (a + b)(a2 - ab + b2)
PROPIEDADES DE POTENCIACIÓN
Producto de Potencias de Igual base: Se deja la misma base y se suman los exponentes
(X3Y5)(X4Y9) = X7Y14
Cociente de Potencias de igual base: Se deja la misma base y se restan los exponentes.
Potencia de Potencia: Se deja la misma base y se multiplican los exponentes
Potencia de un Producto: Cada factor se eleva al exponente dado
(X3YZ4)5 = X15Y5Z20
Potencia de un Cociente: Tanto numerador como denominador se afectan por el exponente dado
Exponente Negativo:
Potencias de cero:
X0=1 0N = 0 00 = INDETERMINADO
POTENCIAS DE 10
100 = 1 101 = 10 102 = 100 103 = 1000 10-1 = 1/10 = 0,1 10-2=1/100 = 0,01 10-3= 1/1000 = 0,001
NOTACIÓN CIENTÍFICA:
Es utilizada cuando se desea expresar una cantidad en términos de potencias de 10, dejando el número original con un dígito en su parte entera
245,47 expresado en notación científica: 2,4547 X 10-2
3645 en notación científica: 3,645 X 103
RADICACIÓN
Corresponde a una expresión cuyo exponente es número racional:
Propiedades de Radicación
- ejemplo:
- ejemplo:
- ejemplo;
- ejemplo:
LOGARITMACIÓN
Es el exponente al que hay que elevar una base para obtener el número dado.
Log39 = 2 porque 32=9 log101000 =3 porque 103= 1000 log0,01= -2 porque 10-2= 0,01 (cuando no se expresa la base debe entenderse como logaritmo en base 10)
Propiedades de los logaritmos
- Log(A X B) = logA + logB
- Log(A/B) = logA – logB
- Logn1= 0
- Lognn= 1
- La base de un logaritmo nunca es negativa
- Los números negativos no tienen logaritmo
FORMULA GENERAL DE ECUACIÓN CUADRATICA
Dada la ecuación general de segundo grado: AX2 + BX + C = 0, la forma general para resolverla es:

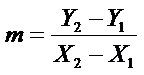
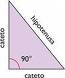
 con vértice en A, son:
con vértice en A, son: